算法记录（二）

Leecode 116 填充每个节点的下一个右侧节点指针

给定一个 完美二叉树 ，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：
填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。初始状态下，所有 next 指针都被设置为 NULL。

java
struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

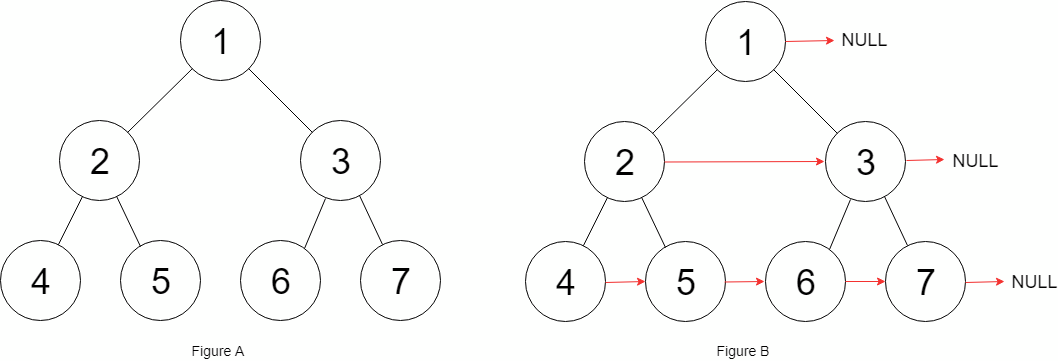
java
输入：root = [1,2,3,4,5,6,7]
输出：[1,#,2,3,#,4,5,6,7,#]
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化的输出按层序遍历排列，同一层节点由 next 指针连接，'#' 标志着每一层的结束。

两种思路，第一种比较好想，就是层序遍历

java
// 层序遍历解法
        if(root == null) return root;
        Queue<Node> queue = new LinkedList<Node>();
        queue.add(root);
        while(!queue.isEmpty()) {
            // 一层的个数
            int size = queue.size();
            for(int i = 0 ;i<size;i++) {
                // 出队
                Node node = queue.poll();
                if(i<size-1) {
                    node.next = queue.peek();
                }

                if(node.left != null) queue.add(node.left);
                if(node.right != null) queue.add(node.right);
            }
        }
        return root;

层序遍历很好理解，就是创建一个队列，然后每次向队列里加入一层，当队列非空，则出队且获得当前队列的元素个数，这个元素个数就是当前这层的个数，然后分别将每个出队的元素的左右孩子加入队列，重复以上步骤，直到队列为空

而在这个题目中，如果根据层序遍历来实现的话，next指针直接指向出队后当前队列的队头即可，当然要注意，如果是当前这一层的最后一个，则直接指向null，好了这道题目就这个解法

那第二种解法就比较巧妙，不用额外的空间，这里是利用了前一个结点创建的next指针

很显而易见，每个节点的两个孩子节点之间可以直接通过next指针相连，而不同节点的两个孩子节点之间就无法直接相连了，这是我们要解决的问题

我们是从上往下进行连接的，这时候我们发现，我们要连接第N+1层的next指针的时候，其实我们是站在第N层的位置进行连接的，换句话说，我们在连接第N+1层的next指针的时候，我们是已经连好了第N层的next指针，所以可以通过第N层的next指针取将不同节点的两个孩子节点相连

即root.right.next = root.next.left
代码如下，这里用的是递归解法

java
// 递归解法
        if(root == null || root.left == null) {
            return root;
        }
        // 将左孩子的下一个指向右孩子
        root.left.next = root.right;
        if(root.next!=null){
            root.right.next = root.next.left;
        }else{
            root.right.next = null;
        }
        connect(root.left);
        connect(root.right);
        
        return root;